The Chaocipher Clearing House
Progress Report #6
Repetitions
in the Chaocipher Exhibits
Greg Mellen [5] has the following
to say about repetitions in Chaocipher:
Repetitions.
Repetitions are in accord with what one expects for random
text.
There is a 5-letter repetition, XXACN, at an interval of 602
characters in lines 122 and 133 in Exhibit 1. The
corresponding
plaintext is different, however, being respectively ESTAB and NISAH.
I
wanted to double-check Mellen's results and ran Exhibit 1 through a
repetition-finding software program looking for repetitions of five
letters or more. Here
are the results:
Repetitions in Exhibit 1:
Plaintext/Ciphertext
+------------------------------------------------------------------------------+
|
|
Line
|
Offset
|
|
Plaintext |
| Repetition +-------+-------+-------+-------+ Distance
+----------+----------+
|
| 1st | 2nd |
1st | 2nd
|
| 1st
|
2nd |
+------------+-------+-------+-------+-------+-----------+----------+----------+
| WQKRXD
| 5
| 138 | 250 | 7538
|
7288 | RLAZYD[O]|
ENHISG[O]| 2*2*2*911
| TXUVO
| 20
| 166 | 1057 | 9125
|
8068 | KBROW[N] |
LPOWE[R] | 2*2*2017
| PQHMN (*) | 22
| 34 |
1159 | 1819 |
660 | OODQQ[U]
|
OODQQ[U] | 2*2*3*5*11
| KNDXD
| 22
| 108 | 1179 | 5909
|
4730 | UMPOV[E] |
THEEA[R] | 2*5*11*43
| LQYMR
| 39
| 95 | 2145 | 5195
|
3050 | ALLGO[O] |
MPOVE[R] | 2*5*5*61
| DLNAA
| 50
| 68 | 2717 | 3690
| 973 |
SJUMP[O] |
ODQQU[I] | 7*139
| MOWLH
| 79
| 92 | 4345 | 5057
| 712 |
ALLGO[O] |
TYWAL[L] | 2*2*89
| XXACN
| 122 |
133 | 6686 | 7288
| 602
| ESTAB[L] |
NISAH[I] | 2*7*43
| ETOSX
| 202 |
240 | 11067 | 13167 | 12100 |
LEWNO[R] |
DHERE[T] | 2*2*5*5*11*11
| EISOT
| 202 |
236 | 11097 | 12929 | 11832 |
TIONS[T] |
DICAT[E] | 2*2*2*3*17*29
+------------+-------+-------+-------+-------+-----------+----------+----------+
(*) Although the plaintexts are in sync, the repeats stop
after five
letters.
The corresponding ciphertexts are
PQHMN[FHX] and PQHMN[MID].
The bracketed letters in the plaintext columns denote the
letter that
follows the repetition. I inserted it to possibly indicate
why the
ciphertexts change at that point.
As it turns out, there are numerous five-letter repetitions,
and
even a six-letter one. If a repetition is meant to denote
identical plaintexts, then only
PQHMN can be considered causal (even the six-letter repeat seems to be
accidental). The strange thing is that, although the
plaintext
continues to be in sync, the ciphertext repetition stops after five
letters. I checked to see where the respective offsets fall
within
13-letter and 26-letter blocking:
1159=2 mod
13 1819=12 mod 13
1159=15 mod 26 1819=25 mod 26
Had the sixth plaintext letter occurred at a block break, that might
have explained it. Alas, it does not.
No
other exhibit displays causal repetitions (see below) except for
Exhibit 5 message 3, which shows a tantalizing five-letter
repetition:
| Repetition | Offsets |
| First | Second |
| ZH | 1 | 67 |
| TK | 8 | 48 |
| TT | 10 | 120 |
| TL | 11 | 156 |
| NV | 19 | 62 |
| YH | 25 | 46 |
| SM | 27 | 149 |
| MG | 28 | 32 |
| XJ | 30 | 122 |
| FL | 43 | 112 |
| XU | 52 | 124 |
| CB | 85 | 142 |
| BBNKF | 105 | 136 |
But there is another reason to conclude that all the repeats
(excluding the one in Exhibit 5 message 3) are
accidental. Cryptologia carries the
article "Kasiski's Test: Couldn't the Repetitions be by Accident?"
written by
Klaus Pommerening [6].
It is an excellent article which
touches on the question "what is the probability of having a repetition
of length R in a message of length M from alphabet size A?" (he uses
the same method used to calculate the Birthday Paradox). I
wrote a
script to compute the probabilities for all five exhibits and got the
following results:
+---------+------------------------------------------------------+---+----------------+
|
|
Repetition
Length
|Max|
|
| Message
+------------------------------------------------------+Rep|
Comment |
| Length |
1
2
3
4
5
6
|Len|
|
+---------+------------------------------------------------------+---+----------------+
| 13336 |
1
1
1.0000
1.0000 0.999437 0.249958 | 6
|
Exhibit 1 |
| 1263 |
1
1
1.0000
| 3 |
Exhibit 2 |
| 910 |
1
1
1.0000
| 3 |
Exhibit 3 |
| 1908 |
1
1
1.0000
0.981204
| 4 |
Exhibit 4 |
| 162 | 1
1.0000
0.516118 0.027116
0.001043
|
5 |
Exhibit 5, #3 |
+---------+------------------------------------------------------+---+----------------+
Results:
- A value of 1 denotes a probability of 100%, while
1.0000 denotes
a number very close to 1.
- We can use 0.5 as the
cut-off point: < 0.5 denotes "rather
unlikely", > 0.5 denotes "rather likely".
- In
Exhibit 1, repetitions of 5 letters or less are most likely to
occur accidentally. The 6-letter repetition has a probability
of 0.25,
but this is a bit too close for comfort. Besides, the
6-letter
repetition has two different plaintexts.
- In
Exhibits 2 the maximum repetition length found is 3, which is
highly likely to occur by chance.
- The same for
Exhibit 3.
- The same for Exhibit 4, whose maximum
repetition of 4 is still
too likely to occur.
- Exhibit 5, message #3 is a
different kettle of fish. There are
12 two-letter repetitions which are probably accidental. The
five-letter repetition has a probability of 0.001+ (one in a thousand)
of occurring. Statistically it is very significant, but it is
not
clear what to do with it.
- Question: can
the plaintext to Exhibit 5 message 3 be found in Stewart C. Easton's
book [7] by
finding a plaintext repetition 31 characters apart?
There
is one thought that I had but I don't think it's feasible.
Looking at the 6-letter repetition in Exhibit #1, let us suppose that,
fortuitously, the Chaocipher machine returned to the exact same
settings both times. The individual letters of the first
plaintext may
have affected the machine in precisely same way as those of the second
plaintext string (e.g., some letters have the influence on the
machine). We could then infer that the following letter pairs
have a
similar effect on the machine:
R <-> E
L <-> N
A <-> H
Z <-> I
Y <-> S
D <-> G
There are two problems with this idea:
- Why wouldn't the "O" in the seventh position extend
the
repetition? Both O's do not come at the end of a 13- or
26-letter
block.
- If the same ciphertext with the
same machine settings can
decipher to different plaintexts then we have a polyphonic-like
ambiguity problem (similar to decrypting Key Phrase ciphers).
If I were more convinced that the six-letter
repetition were causal I'd
feel more confident pursuing this track. Something to bear in
mind in
the future.Coincidences Between the 100 "All Good ..."
Encipherments
I was curious to see if correlating the
coincidences (or "hits") between each pair of the first 100 lines in
Exhibit 1
would produce something of value. These 100 lines are
55-letter
blocks of the identical plaintext beginning "All Good, Quick Brown
Foxes ..." where the comma and period are enciphered as Q and W,
respectively. The expected number or coincidences for two
random
blocks is computed as Kr (pronounced
'kappa-random') times 55 = 0.0385 * 55 = 2.12, while a causal number of
coincidences is Kp ('kappa-plain') times 55 =
0.0667 * 66 = 3.67. The following table shows the lines that
had seven or more hits:
| Line | Number of Hits |
| First | Second |
| 22 | 34 | 11 |
| 8 | 46 | 9 |
| 10 | 88 | 9 |
| 6 | 47 | 8 |
| 11 | 89 | 8 |
| 19 | 34 | 8 |
| 21 | 80 | 8 |
| 31 | 100 | 8 |
| 1 | 92 | 7 |
| 8 | 29 | 7 |
| 9 | 37 | 7 |
| 11 | 39 | 7 |
| 21 | 90 | 7 |
| 23 | 41 | 7 |
| 26 | 95 | 7 |
| 29 | 92 | 7 |
| 31 | 77 | 7 |
| 41 | 83 | 7 |
| 53 | 89 | 7 |
| 55 | 76 | 7 |
| 58 | 86 | 7 |
| 63 | 83 | 7 |
| 77 | 78 | 7 |
| 77 | 80 | 7 |
| 81 | 96 | 7 |
| 82 | 86 | 7 |
| 2 | 24 | 6 |
| 3 | 24 | 6 |
| ... | ... | ... |
| 88 | 92 | 6 |
| 88 | 99 | 6 |
As
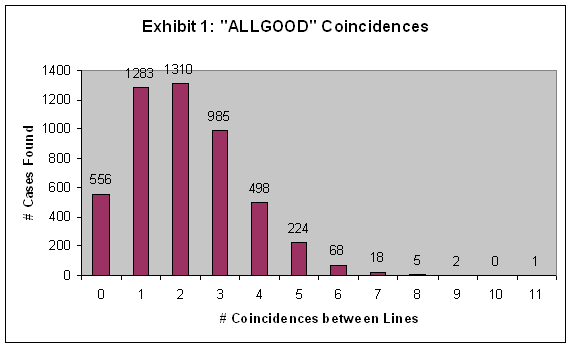
impressive as finding eleven hits may be, graphing the full results
shows the distribution is definitely Poisson:
Using
a Poisson
Calculator with an average rate of success of Kr
* 55 = 2.12 and (100 x 99)/2 = 4950 distinct comparisons, I calculated
the expected number of coincidences:
| Poisson
Calculations |
Number of
Coincidences | Frequency | (o-e)2/e |
Expected
(e) | Observed
(o) |
| 0 | 594 | 556 | 2.43 |
| 1 | 1260 | 1283 | 0.42 |
| 2 | 1345 | 1310 | 0.91 |
| 3 | 943 | 985 | 1.87 |
| 4 | 500 | 498 | 0.01 |
| 5 | 212 | 224 | 0.68 |
| 6 | 74 | 68 | 0.49 |
| 7 | 22 | 18 | 0.73 |
| 8 | 6 | 5 | 0.17 |
| 9 | 1.4 | 2 | 0.26 |
| 10 | 0.3 | 0 | 0.3 |
| 11 | 0.06 | 1 | 14.73 |
| Total | 4957 | 4950 | 22.98 |
Need to find the confidence
interval.
References in the Open
Cryptographic Literature with Relevance to Chaocipher
I
had a thought the other day: are there any covert references to
Chaocipher in the open cryptographic literature? My idea was
that
cryptographic authors may have had Chaocipher in mind while authoring a
cryptographic article or text. Did William F.
Friedman refer
to Chaocipher, even in an oblique way, when writing his "Advanced
Military Cryptography"? Are there any such vague references
in
interviews written up in Cryptologia? So, armed with some
quiet
and a hot drink, I started pulling out and scouring books from my
library. Here are some interesting quotes I found.
William
F. Friedman in Advanced
Military Cryptography
In Advanced Military Cryptography
[1],
written in 1944, William F. Friedman writes the following in paragraphs
72 and 74:
72.
Substitution-cipher machines. -- a.
The substitution
principle lends itself very rapidly to the construction of cipher
machines for effecting it. The cryptographs described in the
preceding two sections [Ed. the Wheatstone cipher and the M-94 device],
as well as the simpler varieties making use merely of two or more
superimposed, concentric disks are in the nature of hand-operated
substitution-cipher mechanisms that are difficult to use, cannot be
employed for rapid or automatic cryptographic manipulations, and are
quite markedly susceptible to errors in their operation. For
a
long time these defects have been recognized and many men have striven
to produce and to perfect devices more automatic in their functioning.
However, the would-be inventors have not, as a rule, realized
the
complexity of the problems confronting them; nor have they approached
these problems with the necessary and thorough knowledge of both
theoretical and practical cryptography, with its many limitations, and
theoretical as well as practical cryptanalysis, with its wide
possibilities for the exercise of human ingenuity.
74. Machines affording
polyalphabetic substitution.
-- a. In recent years there have been placed upon the
commercial
market several cipher machines of more than ordinary interest, but they
cannot be described here in detail. In some of them the
number of
secondary alphabets is quite limited, but the method of their
employment, or rather the manner in which the mechanism operates to
bring the cipher alphabets into play is so ingenious that the solution
of cryptograms prepared by means of the machine is exceedingly
difficult. The point should be clearly recognized and
understood:
other things being
equal, the manner
of shifting about or varying the cipher alphabets contributes more to
cryptographic security than does the number of alphabets involved, or
their type. For example, it is possible to
employ 26
direct-standard alphabets in such an irregular sequence as to yield
greater security than is afforded by the use of 1,000 or more mixed
alphabets in a regular or an easily-ascertained method. The
importance of this point is not generally recognized by inventors.
This
was written some 20 years after Friedman analyzed the Chaocipher (see [2]). I
assume the Chaocipher crossed Friedman's mind while writing these
paragraphs.
- We know from Deavours and
Kruh that Chaocipher is particularly susceptible to
enciphering errors.
- Friedman
probably believed the system was solvable -- Deavours and Kruh [page
193] quote a letter from Friedman to Byrne
around February 1957 where he writes "why
you put in
that book [Ed. Silent Years] the completely extraneous matter of
ciphers when you had so much of interest to tell of Joyce".
It is
obvious that Friedman did not have an ax to grind with Byrne and that
they kept their communication lines open over the years.
- When
Friedman wrote paragraph 74, was he also referring to Chaocipher having
too many alphabets rather than a clever keying sequence?
Lambros
D. Callimahos in "The Legendary William F. Friedman"
In Lambros
D. Callimahos's fascinating article "The Legendary
William F. Friedman" [3]
we find reference to William F. Friedman's standard request for
material from prospective cryptographic inventors, quoted by Callimahos
from Friedman's technical paper "The Principles of Indirect Symmetry
of Position in Secondary Alphabets and Their Application in the
Solution of Polyalphabetic Substitution Ciphers":
A
set of 50 test messages, each 25 letters in length and beginning at the
same initial enciphering juxtaposition, was submitted by Mr. Burdisk.
This
is quite similar to Friedman's request from Byrne, quoted in [2]:
In
a letter, September 7, 1922, William F. Friedman, responding to a
previous question of Byrne's about the type of material he needed to
solve the Chaocipher, said "a series of fifty messages of approximately
twenty-five words each might be sufficient ..."
Notice
the request for 25 words per message for Chaocipher versus 25 letters
from Mr. Burdisk, but the "50 messages / 25 elements"
formula is
still there. Also interesting is that Friedman's request for
"in-depth" messages is phrased as "beginning at the same initial
enciphering juxtaposition". Deavours's and Kruh's messages in
Exhibit 5 fulfill this requirement: they probably begin at the same
machine settings but diverge immediately.
In [3]
Callimahos alludes to an interesting cryptographic machine -- could he
be referring to Chaocipher?
Friedman
studied many proposals for cryptographic systems, embracing both manual
and machine methods, demolishing everything that came his way.
Good cryptographic ideas were hard to come by, as
requirements
were stiff and standards high. ... In another case, an ingenious
machine fractionated a
plaintext letter into two parts,
subjected these fractional parts to a complex substitution, and finally
recombined the parts to produce a single plaintext letter: this was a
brilliant idea that did not long withstand Friedman's scrutiny.
The
following quote from Chapter 21 in Byrne's "Silent Years" [4] makes reference to
'splitting' or fractionating the written word:
In
a preceding chapter I have referred to Rutherford's achievement in 1919
of splitting an atom for the first time. In the preceding
year,
1918, I had discovered a method of doing something to the written word,
in any language, which affected that written word so as to result in
its chaotic disruption.
Could
Callimahos be
referring to Chaocipher, addressing the fractionating nature
of
the mechanism? I know it's a long shot, but in any case it
gives
an interesting direction to pursue with Chaocipher.Misunderstanding
the Byrne-Friedman Relationship
A
casual reader of Byrne's "Silent Years" could be excused for drawing a
negative impression of William F. Friedman in his relationship with
John F. Byrne. In "Silent Years" pp. 275-276 we read the
following:
In
the week
after receipt of this letter [i.e., from Parker Hitt], I arrived once
more with my first model in Washington, where I was met on March 17,
1922, by Colonel Hitt, who immediately escorted me in person to give me
a glowing introduction to both Major Moorman, and Mr. W. F. Friedman,
Cryptanalyst.
Nearly five month later I wrote to
Major Moorman and received the following reply:
. . .
August
26, 1922
. . .
Dear Sir:--
I
have for acknowledgment of your letter of August 21st and wish to
assure you that I have not forgotten the profitable hour we spent
together. I am sending a letter to Mr. Friedman with request
that
he communicate with you with reference to your cipher device.
Very
sincerely yours,
Frank Moorman
Major, General Staff
And
a few days afterwards I received by parcel post from Washington a
package containing my cipher model smashed into smithereens.
The
reader might conclude that Friedman or the military establishment were
vindictive thugs out to impede any progress Byrne might make.
Curiously, Byrne omits a letter Friedman sent him on
September 7,
1922, just twelve days after Moorman replied to Byrne:
In a letter,
September 7, 1922,
William F. Friedman, responding to a previous question of Byrne's about
the type of material he needed to solve the Chaocipher, said "a series
of fifty messages of approximately twenty-five words each might be
sufficient ...". [2]
We
can assume that the package Byrne received from
Washington contained his cipher machine (broken in transit?) and a letter from Friedman
requesting cipher material according to Friedman's standards.
Byrne does not tell the reader about Friedman's request,
nor whether he sent the requested ciphertexts, nor whether
Friedman
succeeded in breaking the requested material. In my opinion,
Byrne's narrative unfairly lacks all the facts. His
side of
the story leaves us with the feeling that he wrote more to
ease
his own feelings about Friedman and the military than to set the record
straight.Locating
the Plaintext to Exhibit 5, Message 3?
What
can we make of the five-letter, highly causal repetition found in
Exhibit 5 message 3? I believe it should be examined more
closely. I wondered whether we could place message 3 in
Easton's
book by locating a five-letter plaintext repetition at a distance of 31
characters. A cursory examination in chapters 1 and 2 found
such
repetitions, but the resulting plaintexts are not complete sentences,
or
even word-complete (i.e., begin and end with complete words).
The
closest match (at offset 8457 in chapter 2) began at the beginning of a
sentence but was cut off at the end:
"HOWTHERAIL"
and "HOWTHELOCA" at offset 8457
PT:
ATTHATEARLYAGEHELEARNEDBYIMITATIONANDEXPERIMENTATIONQSPURREDONBYHISINTERESTINTHEM
CT:
JZHASQNRTKTTLZDYOWLNVDMWNYHSMGXJMGZQTHRIWTIFLXYHTKBOXUYEANJUDXNVOGFZHMJEGRDGGPUGS
PT: ECHANICSOFHUMANACTIVITYHHOWTHERAILWAYSTATIONWASMANAGEDQHOWTHELOCALFLOURMILLOPERAT
CT: XVBACBEPKWHVSBIJGOHKVKAIBBNKFHFFLSFMIINTTXJXUHWQAPTSNBTBBNKFUCBPIONQSMVEHUXTLMRRA
^^^^^
^^^^^
I hope to continue
examining this phenomenon.References
[1]
Friedman, William F. Advanced Military Cryptography.
Aegean Park Press, 1976.
[2]
John Byrne, Cipher A. Deavours and Louis Kruh. Chaocipher
enters
the computer age when its method is disclosed to Cryptologia
editors. Cryptologia, 14(3): 193-197.
[3]
Callimahos, Lambros D. The
Legendary William F. Friedman.
Cryptologic Spectrum, Winter 1974, Volume 4 Number 1.
Reprinted in Cryptologia, July 1991 (pp 219-236), and
available
as an NSA declassified document at http://www.nsa.gov/public_info/_files/cryptologic_spectrum/legendary_william_friedman.pdf.
[4] Byrne, John F.
1953. Silent Years. New York: Farrar, Straus
& Young.
[5]
Mellen, Greg. 1979. J. F. Byrne and the Chaocipher,
Work in Progress. Cryptologia, 3(3): 136-154.
[6] Pommerening,
Klaus. Kasiski's Test: Couldn't the Repetitions be
by
Accident? Cryptologia, October 2006, 30(4): 346-352.
[7] Easton, Stewart C. Rudolf Steiner: Herald of a New
Epoch. Anthroposophic Press. 1980.
Copyright
(c) 2009 Moshe Rubin
Created:
20 March 2009
Last updated: 30 September 2009