The Chaocipher Clearing
House
Progress Report #7
Comments
from Readers
Since
starting the Chaocipher Clearing House I have received numerous
responses from readers. One of these is Jeff Calof.
With
Jeff's permission I would like to upload some of the e-mail thread
we've been conducting.
| Received 11
March 2009 |
Hi
Moshe,
Great
analysis and written summarization of your work on
Chaocipher. I,
too, have enjoyed(!) the challenge of Byrne's ingenious scheme.
After
reading Kruh's Cryptologia Article, I noted that in Exhibit 5 - Message
#3 the ciphertext string BBNKF appeared twice. Once as a
complete, independent block, the other as as split block (TBBNK
FUCBP). Interestingly, this Message has an anomaly as
presented
in the article - namely, while all other full blocks are 5 characters,
this one contains a 4 letter block (UHWA) between the 2 instances of
BBNKF. I can't determine if this was an error during the
writing
of the article (i.e., a character got inadvertently dropped) or an
intended ciphering decision. If intended, then there are 29
characters between the two occurrences (From the 2nd B in BBNKF to the
first B of the next instance). If a 5th character was left
out of
the noted block, then you'd have 30 characters between the BBNKF
occurrences.
It's unlikely that such a 5-character
string would occur entirely randomly. ...
Keep
up the good work - I wonder if Byrne Jr., Kruh and Deavours will ever
divulge what they know (Non-disclosure agreement notwithstanding)?
Jeff
Calof |
| Sent
13 March 2009 |
Hi
Jeff,
First
off, thank you very much for your kind words. The best
compliment
you could give me is that the site is of value to you. I had
a
feeling that much more Chaocipher research was being done but there was
no focal point. From the responses I'm getting I believe this
is
true. I hope you will take part in this global
effort. I
look forward to any other comments, research, etc. you may have.
Truth
be told, I had not noticed the 5-letter repetition -- thanks for
pointing it out. I'd like to compute the probability of such
an
occurrence. The other four exhibits do not show any causal
repetitions (Mellen points out a 5-letter repetition, XXACN, in Exhibit
1 but notes that the plaintexts are different, so the repetition is
non-causal). Could Deavours and Kruh have knowingly selected
a
plaintext so that an underlying plaintext repetition *was* duplicated
in the ciphertext? I hope to pursue this repetition in the
future
and look forward to any research you may do on it.
. . .
You
mention that there is a 4-letter block, UHWA, in message #3. You may
have lost a letter while transcribing or scanning the message
in.
The article clearly shows:
... TTXJX UHWQA PTSNB ...
Therefore
the distance between the repetitions is 31. The repetition is
definitely not expected and should be examined carefully. . .
. I
agree with you that Byrne may have used gear-like sequences or cipher
alphabets whose periods are prime to each other. This may be
what
he meant when he wrote that the ancient Egyptians and Babylonians could
have been completely familiar with the principle.
Regarding
Byrne, Deavours and Kruh divulging the mechanism, I asked Deavours and
Kruh this same question in a recent e-mail to them (they haven't
answered yet). In my opinion there is no commercial value in
Byrne's system given the power, security, and ease of public-key
systems today. In this light Byrne would do best to publicize
the
system. The cryptologic community will verify whether it has
any
commercial value.
Thank you once again for you kind
words and for taking the time to write them. I look forward
to hearing from you again.
Best regards,
Moshe
Rubin |
After
uploading Progress Report #6 I received this e-mail from Jeff (20 March
2009):
Hi
Moshe,
Great
article today... I especially took note of the Callimahos article and
excerpts. The "fractionate" reference supported something
I've
always suspected was a missed clue from Byrne - but seeing this
supports my suspicion.
On
Page 265 of "Silent
Years", Byrne writes:
"The
ancient Egyptians and Babylonians could have been completely familiar
with the principle, a fact which is readily deducible from a treatise
on mathematics written by Hero of Alexandria in the second century B.C"
I
believe this reference is to Hero, or Heron's, treatise
"Metrica". The highlight of this is the Babylonian method for
finding Square Roots (also known as the Heron Method).
Considering other facts Byrne tells us of Chaocipher, this offers some
possibilities for the method. Byrne writes:
Page
266 - "If
every person on earth were to encipher the same message, say for
instance, this paragraph of which this sentence is a part, no two of
the resultant encipherments would be alike"
This
seems to
indicate a Cipher Key is at play somehow; if every
Encipherer's
key were the non-repeating decimal Square Root fraction sequence of
some uniquely chosen non-pure Square number, this would meet Byrne's
criteria.
What could each Encipherer use for their
base #?
Their birth date (MM/DD/YEAR) is nearly unique; their name
less-so but could be numerically represented. Or some other
agreed-upon # between Sender/Receiver.
My problem
with this,
however, is something that Byrne writes, and Kruh and Deavours seem to
substantiate - namely, is this something one would consider "Simple":
Byrne
Page 264 - My method for splitting the word is so simple that it could
be performed by any normal 10-year-old school child
K&D
(2nd Page) - Byrne showed Deavours and Kruh how the Chaocipher worked.
They were quickly impressed with its simplicity, ease of operation and
security
For 1918, I wonder if reducing any number
to its
non-repeating square-root value by hand would be considered "Simple" -
probably not.
Keep up the great analysis... I'm
greatly enjoying your insight and progress.
Sincerely,
Jeff
Calof |
Here's
my response to him on 21 March 2009:
Hi
Jeff,
Many
thanks (again!) for your very kind words (I wasn't sure if you received
my reply on 13 March to your first e-mail, so I'm attaching it just in
case). It's great to hear from one's peers, especially on a
subject we're both highly interested in. I know my progress
reports are circling around the target, but I get a strong feeling that
they're homing in on it. My thoughts are becoming clearer and
more focused re Chaocipher the more I commit thoughts to
paper. I
hope I can help others like you to see your ways clear to solving this
challenge.
<< The
"fractionate" reference supported something I've always suspected was a
missed clue from Byrne - but seeing this supports my suspicion
>>
I'm
glad to hear you've thought along the same lines. I'm
wondering
how two concentric disks can be used to fractionate a letter and
recombine it again. Any ideas? There is a
difference
between Byrne and Callimahos: Byrne refers to splitting a word while
Callimahos refers to fractionating a letter. They might be
referring to the same thing ...
<< I
believe this reference is to Hero, or Heron's, treatise "Metrica". The
highlight of this is the Babylonian method for finding Square Roots
(also known as the Heron Method) >>
Your
idea is a
valid one, as there is an infinite number of numbers whose square roots
are irrational. I believe there was also a "letter of
influence"
element in the cipher, so two people using the same seed number N would
diverge almost immediately based on the plaintext, fulfilling Byrne's
description of an infinite number of keys. Vis-a-vis
Chaocipher,
such a system would have to address the following:
* As you say, it would have to qualify as "simple".
* We know the system fit in a cigar box. Could Byrne have
created
a square root calculator in some form?
* It would
have to explain the "pt/ct identities > 9" phenomenon in Exhibit
1. Can you think of such a scheme?
In my
reply to you last
week I thanked you for pointing out the highly significant repetition
in Exhibit 5, Message 3. It was your observation that
launched
into investigating the repetition in the exhibits. (I pointed
out
that you may have dropped a letter accidentally when transcribing the
message.) I'd like to thank you again . . .
Regarding
the
Exhibit 5 repetition, as I wrote, it certainly looks highly
significant. I'm wondering what one can do with it.
It has
a distance of 31, so you have your prime number theory back again
<g>.
Once again, Jeff, thank you so
much for following my
progress reports and for taking the time to write. It's a
great
feeling knowing others are enjoying them.
Best
regards and looking forward to hearing from you,
Moshe
P.S.
You might find NSA's Declassification Initiative page of general
cryptologic interest: http://www.nsa.gov/public_info/declass/index.shtml |
Distributions
Although
no obvious period is evident in the exhibits, I've been wondering
whether the machine returns to its starting settings at some point.
If it did, we would have two or more "in depth" messages from
Exhibit 1 itself. I decided to shift Exhibit 1 against
itself,
one place at a time, correlating the number of pt/ct matches.
This differs from a regular coincidence test because we have
both
the plaintext and ciphertext.
So, for example, we
encounter this portion of juxtapositioning with
a shift of 182:
1: ALLGOODQQUICKBROWNFOXESJUMPOVERLAZYDOGTOSAVETHEIRPARTYW ...
CLYTZPNZKLDDQGFBOOTYSNEPUAGKIUNKNCRINRCVKJNHTOAFQPDPNCV ...
2: NFOXESJUMPOVERLAZYDOGTOSAVETHEIRPARTYWALLGOODQQUICKBROW ...
OWHKECRMLYWIQIFIKSCYJGCVXNSKYHRYVYEDSZRIFFZAQNHSOMJPORW ...
We
would only count one coincidence here, i.e., the O/Y pt/ct pair.
Even though many plaintext letters coincide between the two
sequences, only a full pt+ct match is counted here.
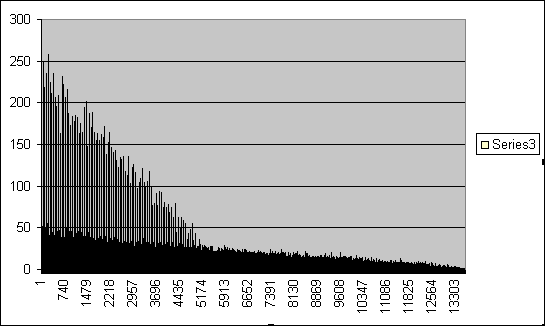
Here's
the resulting graph:
The
first time I saw this graph I was amazed by the tall lines in the
left-hand side of the graph. They were precisely 55 positions
apart -- was I on to something?! The mystery was solved: the
"All
good, quick" phrase is exactly 55 letters long. Having 100
such
phrases greatly raises the probability of a non-causal pt+ct
coincidence. If we ignore these spikes, the graph looks
non-causal, with the number of coincidences slowly decreasing as the
number of overlapping letters decreases.
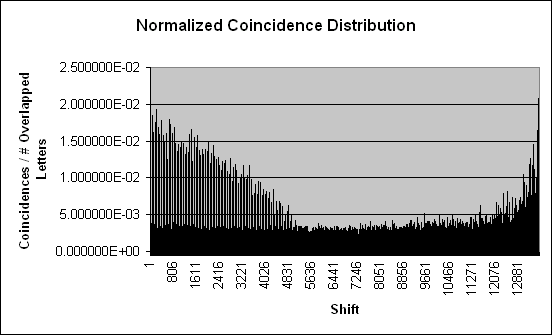
Just to
drive the point
home, I normalized the preceding graph by dividing the number of
coincidences by the number of overlapping letters:
The
rise at the end is to be expected: with relatively few overlapping
letters, the graph becomes much more sensitive to coincidences.
Conclusion:
I cannot identify a point where the machine returns to its original
settings by examining coincidences.
Experimenting
with Cipher Disks
From
descriptions by John F. Byrne and Henry E. Langen
the
Chaocipher
involves two concentric (?) cipher disks with mixed alphabet components
on the rims. After trying to mentally imagine what Byrne may
have
discovered I decided to make myself a cipher disk. I was
unable
to find a suitable template for a 26-letter cipher disk so I wrote a
quick-and-dirty program to draw them for me. I've uploaded a PDF file
containing a
template with three successively smaller disks and wrote some instructions.
To
make your own cipher disk:
- Print out the
page
- Cut out the two largest disks
- Write
the alphabet components on the disk rims
- Get a
piece of corrugated cardboard of, say, 6 inches by 6 inches.
- Stick
a pin through the centers of the disks, connecting them to the
cardboard.
That's all there is to it.
Here's a picture of the one I made myself:
Having
a physical cipher disk has helped me work on the question: how can one
create a sophisticated cipher from a cipher disk. I've learned a lot by
just fiddling around with the cipher disk.
In an
upcoming progress report I'd like to share with you some of
the
schemes I've come up with to create sophisticated ciphers from a
standard cipher disk. I highly advise reading F. L. Bauer's [6]
chapter 3 ("Encryption Steps: Simple Substitution") and chapter 7
("Polyalphabetic Encryption: Families of Alphabets") to get a basic
mathematical basis for dealing with alphabets: shifted, rotated, power
alphabets, cyclic notation, iterated substitutions, mixed alphabets,
and more.
Thoughts About the Chaocipher Mechanism
To
date
I've assumed the Chaocipher is a cipher disk with mixed alphabetic
components, with the disks advancing according to some quasi-random
order. In the background is the fact that Exhibit 1 displays
the
"pt/ct identities > 9" phenomenon -- any candidate mechanism has
to
explain how this could happen. I have been able to conceive
ways
to produce a sophisticated cipher from a cipher disk (see below).
Nonetheless, I returned to Byrne's own description in Silent
Years to try and determine what he had in mind.
Here
are quotes I believe are relevant to the question:
(A) "The
ancient Egyptians and Babylonians could have been completely familiar
with the principle, a fact that is readily deducible from a treatise on
mathematics written by Hero of Alexandria in the second century B.C"
[1, page 265]
(B) "The
first device, or machine, which I constructed solely for the purpose of
demonstrating a principle, was a little model, constructed in an empty
cigar box which, when full, had contained fifty small Havana cigars.
I made this model myself, and to sat that it was a crude
affair
would be only to describe it accurately." [1, page 265]
(C)
"I
then approached several machine makers asking for an estimate of the
cost of making my machine, and from not one of them could I get
anything approaching a firm bid, everyone of them was vague, and the
best I could get by way of an estimate was that it would not be less
than $5,000 and might run to $10,000 or more; ..." [1,
page 267]
(D) "As
to the principle of the machine, it is undoubtedly a most ingenious and
effective device ..." [1, page 273, letter from Colonel
Parker Hitt]
(E) "When
I read Colonel Hitt's letter, it was clear to me that he had not at all
fully comprehended the principle of my "machine", as he called it."
[1, page 273]
(F) "And let me add that
devices far
more operable than my crude model could be mass-produced to sell at ten
dollars each." [1, 282]
(G) "... but he did not
bring the
cipher machine 'explaining that it was too heavy and cumbersome.'"
[2, page 194].
Here are some thoughts:
- Quote
(A) hints that the principle is a mathematical one (rather than a
physical one) and could be inferred from Hero of Alexandria's
mathematical treatise. I checked out Michael Lahanas's site "Heron
of Alexander"
for ideas of Heron's writings. The treatise on mathematics
Byrne
refers to was probably "Metrica", a collection of three books for the
determination of areas and volume of objects. The first two
books
deal with areas and volumes. Book three deals with, among
other
things, his square root extraction formula (here's a summary
of his mathematical ideas).
- Heron
invented gear-related machines (for example, his taximeter, odometer,
and Baroulkos (here
and here))
which could certainly have been the basis of a cigar-based machine.
Nonetheless, Byrne states clearly that the principle is
deducible
from a mathematical
treatise, not a mechanical treatise.
- See Jeff Calof's
e-mail above
with his idea that Byrne may be referring to the square root extraction
method.
- Quote
(B) hints that the machine was a small, simple one, capable of fitting
into a small cigar box. On the other hand, quote (C) tell us
that
the machine makers quoted a relatively huge sum to produce it.
This would infer that the machine was not as simple as, say,
two
concentric disks on a spindle.
- It looks like we're
talking about some mechanical feature.
- In
quote (D), Parker Hitt is impressed with the concept (which Byrne
believes he didn't 'get'). If it were a simple cipher disk, Hitt would
not have been so lavish in his praise.
- In
quote (E) Byrne
puts the word "machine" in double quotes. As if to tell us
that
he did not consider his principle worthy of being called a "machine".
- In
quote (F) Byrne suggests his device could be mass-produced for no more
than ten dollars. Does this imply that the mechanism is not a
very complicated one?j Having said that, quote (G) seems to
imply
that the final device was way to large and expensive than Byrne thought
at first.
Greg Mellen [3] has an enlightening
discussion on this same question in which he infers the
following:
- He shows the diagram of the Baroulkos
by Heron but says "I can think of no way to use it in a
serious cryptographic system".
- He dismisses the use
of continued fractions and "Egyptian Fractions".
- He
says that irrational and transcendental numbers offer other
possibilities (see Jeff
Calof's comment
above), but would be surprised if Byrne knew how to derive the
functions, and how he could implement the function in a cigar box.
- In
1938 Byrne built a second model for demonstrating to the Navy.
"We are not told if it was in a cigar box, but it was a
'working
model on which I could do extended encipherments and decipherments, and
on which I could with some freedom put my principles into operation'".
- From
"extended" Mellen inferred that Byrne's machine can be built in
different "sizes", possibly involving blocks of plaintext, the length
of the block being determined by the size of the machine.
- "With
some freedom" may imply that a small machine does not permit full
exercise of the cipher algorithm.
- "Working
model" may imply that Byrne's initial device was non-functional, useful
for clarifying his concept but only a "paper model".
- In
the sentence [1, page 277] "Working through the summer and
fall of 1937, I made my model and prepared on and by it, a
document I intended for submission to the Navy department
...", Mellen
understands the phrase "on and by it" to mean that there is
interaction of some kind between the machine's enciphering operation
and the key or the plaintext, or both.
- He
uses this, and
the phrase "readily operable machine" [1, page 267]", to explain that
Byrne could not apply for a patent years earlier. Mellen
assumes
that Byrne had no realizable embodiment of his principle, only a crude
model.
- I'm not convinced that "on and by it"
implies some
special type of interaction. Byrne's narrative tends to be
precise but sometimes florid. The phrase might imply that he
was
able to fully encipher his text on it without too much manual
intervention.
- Mellen write
[3, page 141] "I made
paper models of rotors machines which I thought I could (and hence
Byrne could) build in a cigar box. I ruled out complex
gearings,
or gearing of any sort, as being incompatible with "bits of string and
odds and ends." I hope to expand at a later time
on
sophisticated
uses of a standard cipher disk.
In summary,
possible ideas to pursue are:
- A
mathematical concept that could be used to produce a multiplicity of
alphabets or a quasi-random keying sequence, e.g., decimal expansion of
irrational or transcendental numbers, etc.
- Sophisticated
usage of a standard cipher disk
- A gearing system
(as per Hero). This brings to mind the
Wheatstone, Pletts, or Wadsworth devices [5] (which was not used by
Byrne in their classic form).
The
Wheatstone Cryptograph: Could it Help?
In
the previous section we discussed the possibility that Chaocipher is
based on some internal gearing. This brings to mind the
Wheatstone, Pletts, or Wadsworth cipher devices. I intend on
working my way, in an orderly fashion, through William F. Friedman's
analysis of the Wheatstone device [7].
Although this is not
the
Chaocipher mechanism, I hope to (a) widen my cryptanalytic skills, and
(b) hopefully get an insight into possible Chaocipher mechanisms.
Alphabet
Cycle Decomposition
I
referred above to a more sophisticated use of a standard cipher disk.
Although I will have to put it off to a later date, here is
the
output of the program that generated the two alphabets for my standard
cipher disk:
|
1]
hwmdgyceinzvspjfluorxqtakb
2] sbpuiagwlczfredohxmqytvnjk
hwmdgyceinzvspjfluorxqtakb
--------------------------
sbpuiagwlczfredohxmqytvnjk
bpuiagwlczfredohxmqytvnjks
puiagwlczfredohxmqytvnjksb
uiagwlczfredohxmqytvnjksbp
iagwlczfredohxmqytvnjksbpu
agwlczfredohxmqytvnjksbpui
gwlczfredohxmqytvnjksbpuia
wlczfredohxmqytvnjksbpuiag
lczfredohxmqytvnjksbpuiagw
czfredohxmqytvnjksbpuiagwl
zfredohxmqytvnjksbpuiagwlc
fredohxmqytvnjksbpuiagwlcz
redohxmqytvnjksbpuiagwlczf
edohxmqytvnjksbpuiagwlczfr
dohxmqytvnjksbpuiagwlczfre
ohxmqytvnjksbpuiagwlczfred
hxmqytvnjksbpuiagwlczfredo
xmqytvnjksbpuiagwlczfredoh
mqytvnjksbpuiagwlczfredohx
qytvnjksbpuiagwlczfredohxm
ytvnjksbpuiagwlczfredohxmq
tvnjksbpuiagwlczfredohxmqy
vnjksbpuiagwlczfredohxmqyt
njksbpuiagwlczfredohxmqytv
jksbpuiagwlczfredohxmqytvn
ksbpuiagwlczfredohxmqytvnj
(ancgilhsrqtvfompewbkjduxy)
(z)
(bselxtnzfh) (ajoqvryg) (cwpdi) (mu) (k)
(clmizrtjhpoywuqnfxve)
(aksd) (b) (g)
(asotkbphuylqjxnrvdgwifm) (ez) (c)
(abutshirnefqkpxjmglyczdw)
(ov)
(apmwgcfyzondltbierjqsxkuvh)
(aunojyftpqb)
(crkid) (lvxsm) (gzh) (e) (w)
(bgfvmcedzx) (pyrsq)
(aiok) (hwln) (jtu)
(bwcdfnxptihljvqukgr) (eosy)
(mz) (a)
(agehcoblkwzqixust) (drpvy) (fjnm)
(awfklsvtgdeximrubchzyopnq)
(j)
(albztwriqgoupjkcx) (fsnyh) (em) (d) (v)
(acmdoiyxghr)
(kzvntlp) (eqw) (bf) (js) (u)
(aznvjbrgxwdheymo)
(cqluit) (fpsk)
(dxlivkrwogmh) (betzjp) (afu) (cyq)
(n) (s)
(bdmxctfinjugqzkevs) (arl) (how) (p) (y)
(bolgytrcv)
(aenkdqf) (puwxzs) (ij) (h) (m)
(adyvpikocnsulwmqrzbhxfgtej)
(bxrfwqekhmyn)
(cjgvu) (aozp) (dt) (is) (l)
(ahqdvibmtoflckxes)
(gnp) (jwy) (uz) (r)
(axdnufcsgjlzipwthykmv) (bqore)
(amniurdjcbyswvgkqhtxoeplfz)
(btmjzgslrodky)
(aqxhvwn) (cp) (eu) (f) (i)
(aypzwjfrhngbvlei)
(cuds) (ktqm) (o) (x)
(atyuohjrxmszldbnwkvcigpfe) (q)
(bjeguhknloxqyiwsfdprm)
(avzc) (t)
|
You
can see the following:
- two generated
pseudo-random alphabets
- a
tableau consisting of one alphabet as the stator and the other alphabet
shifting on position at a time, producing 26 enciphering alphabets
- the
cycle notation for each of the 26 alphabets mentioned in the previous
bullet
In
an upcoming progress report I'll discuss how we can use the cycle
notations to demystify and simplify working with a cipher disk.
References
[1] Byrne, John F.
1953. Silent Years. New York: Farrar, Straus
& Young.
[2]
John Byrne, Cipher A. Deavours and Louis Kruh. Chaocipher
enters
the computer age when its method is disclosed to Cryptologia
editors. Cryptologia, 14(3): 193-197.
[3]
Mellen, Greg. 1979. J. F. Byrne and the Chaocipher,
Work in Progress. Cryptologia, 3(3): 136-154.
[4] Kahn, David.
1967. The Codebreakers: The Story of Secret
Writing. Macmillan.
[5] Louis
Kruh. The Mystery of Colonel Decius Wadsworth's Cipher
Device. Cryptologia, 6(3): 238-247.
[6]
Bauer, Friedrich. L. 2000. Decrypted Secrets:
Methods and
Maxims of Cryptology (2nd ed.). Berlin: Springer.
[7]
Friedman, William F. Several Machine Ciphers and Methods for
their Solution. Riverbank Publication Volume 2, No. 20.
1918. Reprinted by Aegean Park Press, 1979.
Copyright
(c) 2009 Moshe Rubin
Created:
3 April 2009
Last Updated: 22 November 2018